Is there a limit to athletes’ abilities in athletic running events?
I’m forming a group of students and grads interested in data analysis: The MI^2 (square) Group. The name comes from the fact that we have students from MIM University of Warsaw and MINI Warsaw Technical University. We are playing with different projects and ideas. Today you will read about one of them. The article below is prepared by Witold Chodor and it’s a summary of his bachelor thesis (here you will find the thesis, it’s in polish).
Predicting athletes’ abilities in athletic running events
A lot of people ask themselves a question what the limits of athletes’ abilities are and how long they will be still capable of beating another records. The question had frequently crossed my mind as well. When I came across an article of D.C. Blest entitled ”lower bounds for athletic performance” which was written in 1996, I decided to investigate this issue more thoroughly by using more extensive data.
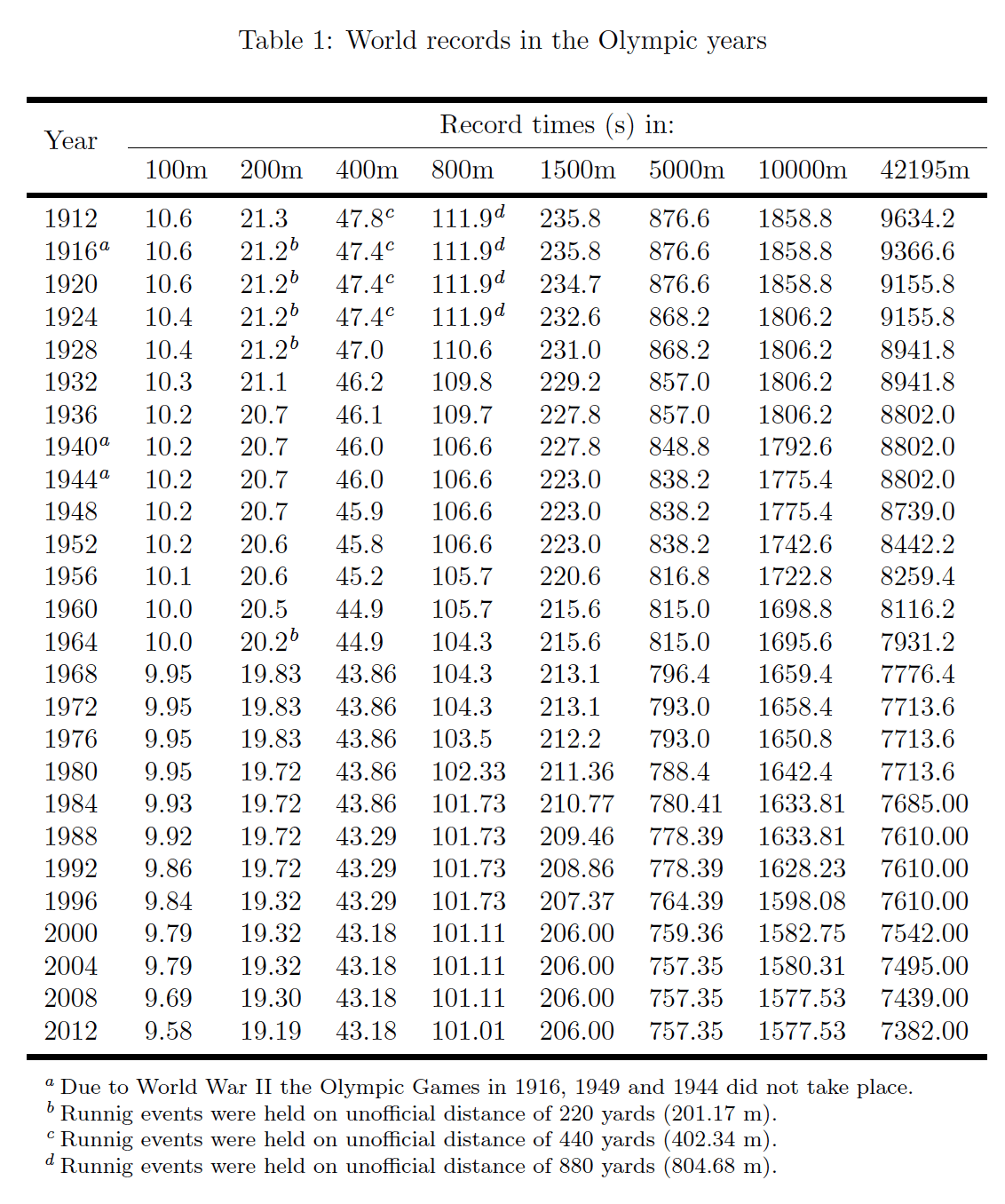
In my work I was trying to find predictions of athletes’ abilities running the following eight distances: 100m, 200m, 400m, 800m, 1500m, 5000m, 10000m and 42195m (the so-called marathon). In the investigated sample there were record times achieved on above-mentioned distances. I assumed to use the records only from the Olympic years, beginning in 1912 and ending in 2012.
Modeling athletes’ performances
Let us assume that i-th row of the table 1 shows the Olympic year (i ∈{1,…,n}, n – number of the Olympic games) while j-th column (except for the first) shows the subsequent distances (j ∈{1,…,m}, m – number of
distances).
Initial data analysis brought to my mind the idea of describing the investigated sample by using power law model for the i-th Olympic year
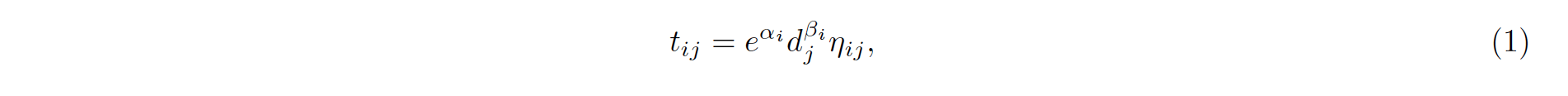
where:
| tij | – record time achieved in the i-th Olimpic year during a j-th distance run, | ||
| dj | – j-th distance, | ||
| αi,βi | – power law model parameters for the i-th Olympic year, | ||
| ηij | – random element with a distribution ηij ∽ logN(0,σ2), for fixed i ηij are independent, |
At this moment the main task was to find the estimates of the parameters αi and βi. It became much easier after having found the logarithm of both sides of the equation (1). As a result, for the i-th Olympic year I obtained linear model
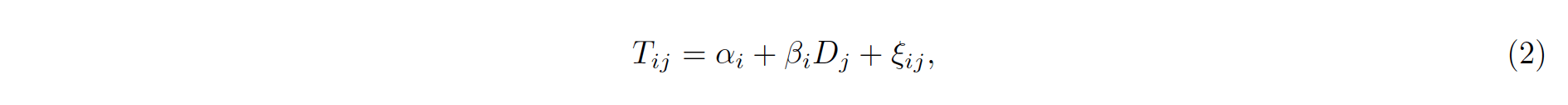
where:
| Tij := ln(tij),Dj := ln(dj),ln(ηij) := ξij. |
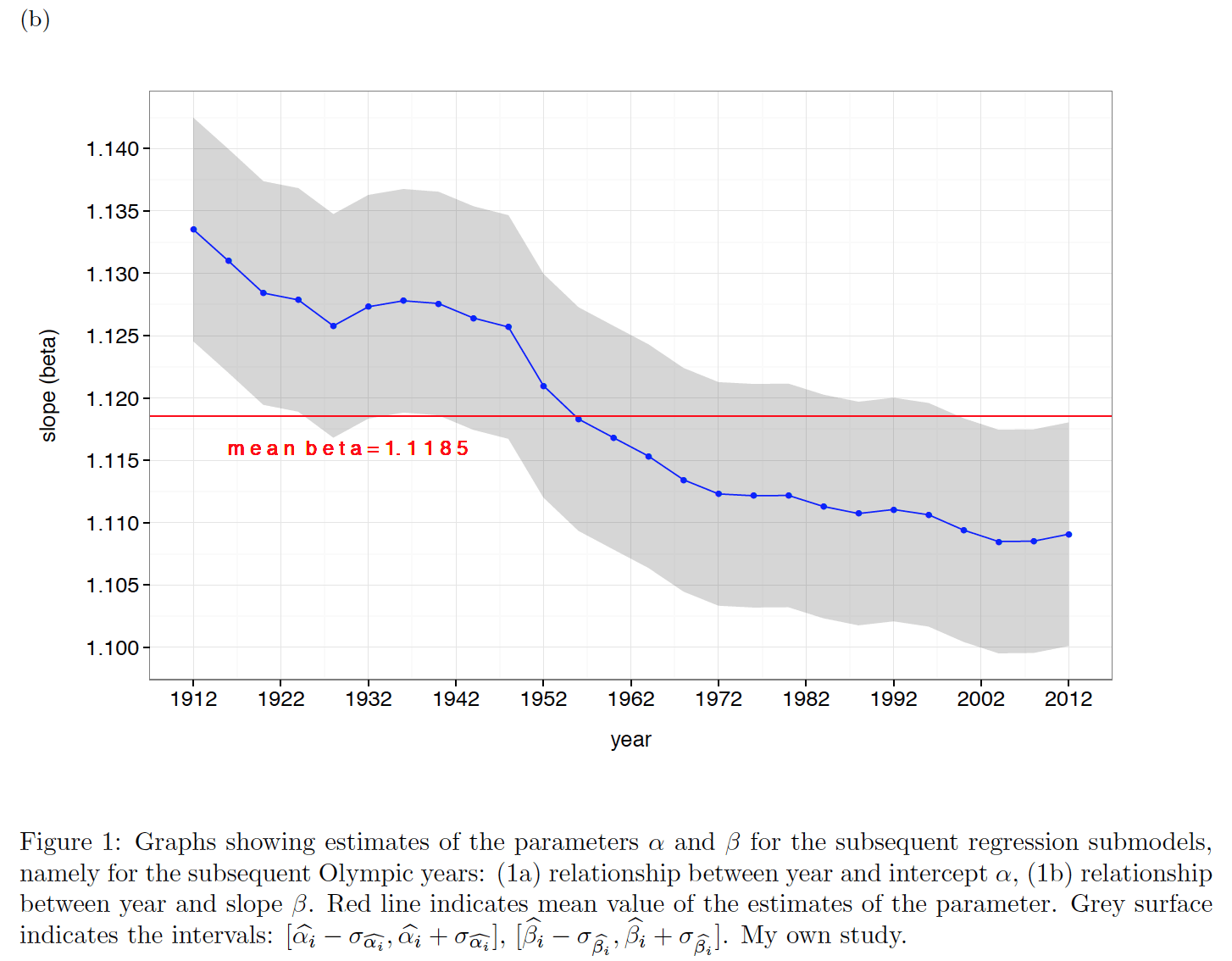
With the use of the R statistical software I managed to find estimates of the parameters α and β. Both Figures (1a) and (1b) show how values of the estimates of the parameters change in the subsequent Olympic years. It is worth considering the fact that the mean value of the intercept estimate stays within all CI intervals.
I will remind that my intention was to find critical values T∞,j for each of the eight distances. It would be easier if I were to estimate the value of only one parameter of the model. I assumed that, therefore, for each i ∈{1,…,n}
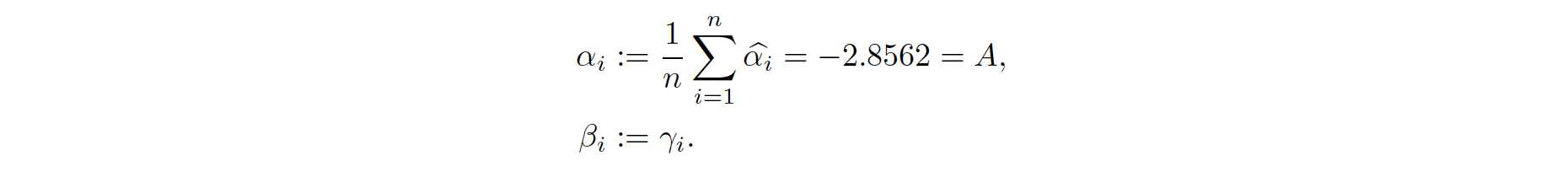
Then model (2) took the following form
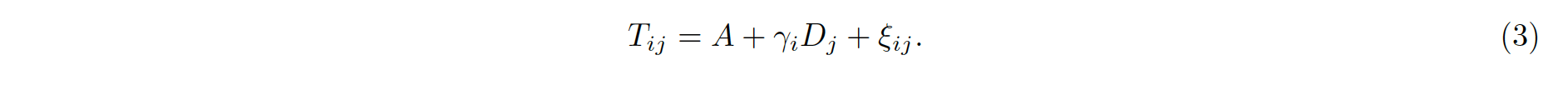
Formally speaking the model (3) is the model nested in the model (2). Likelihood ratio test for these two models allowed me to state that the alternate model is not significantly worse than the model (2). This is why I used the alternate model in the next step of my data analysis.
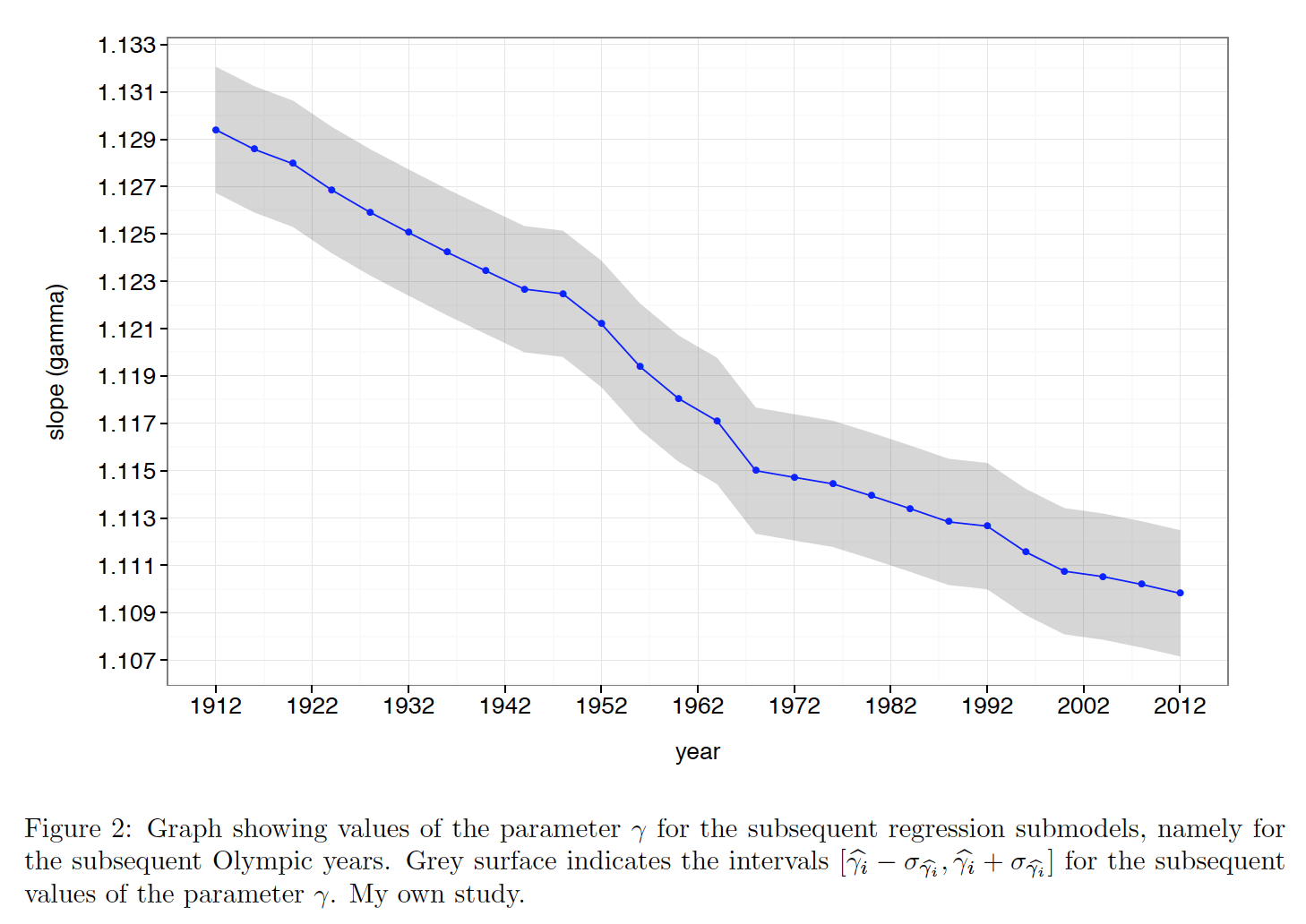
Once again I used R program to find estimates of the parameter γ. In the figure 3 we can clearly see that the subsequent values of the parameter γ form a strictly decreasing sequence. It is obvious that they are greater than zero for Tij and Dj are positive (even grater than one – we should not expect that the athletes will start to run longer distances with an average speed greater than in shorter ones). These two pieces of information allowed me to state that the limit γ∞ has to exist.
Prediction of the limits of athletes’ abilities
In this part of my thesis I was supposed to find a nonlinear curve which will fit the values of the parameter
γ the best. Having such a curve, I was able to determine critical value γ∞. I introduced the following notation:
| xi | – explanatory variable which is the number of the i-th Olympic Game, xi are independent, | ||
| yi | – explained variable which is the value of the estimate of the parameter γi for i-th Olympic Games, | ||
| φ | – vector of the unknown parameters φ = (φ1,…,φp), | ||
| f | – nonlinear function on account of at least one parameter φi, | ||
| εi | – random element with the distribution εi ∽N(0,σ2), εi are independent. |
Then I obtained a nonlinear model of the following form
| yi = f(xi,φ) + εi. |
I took into account 7 different nonlinear models, of which, as it occurred, the antisymmetric exponential model (figure 4) fits γi the best.

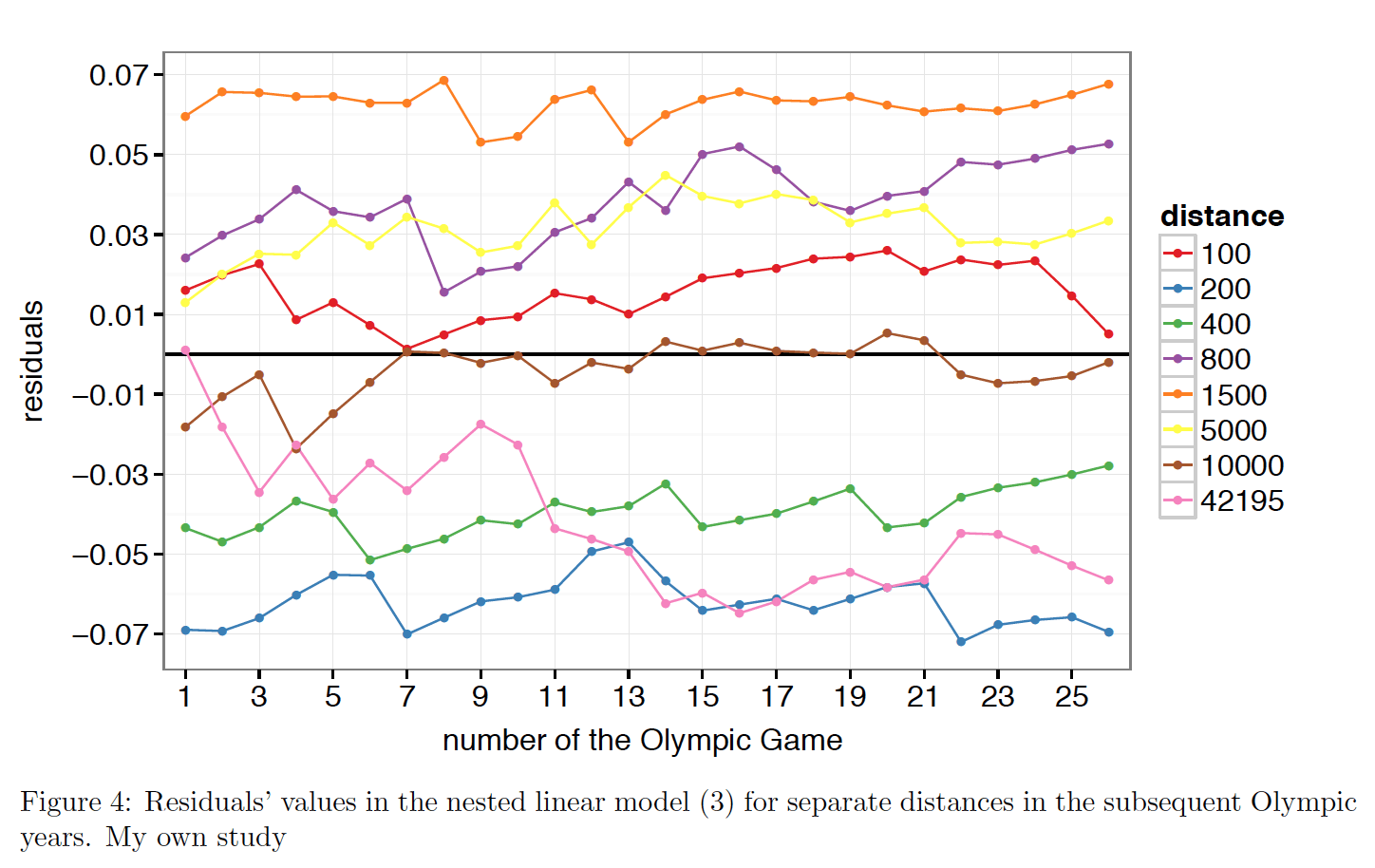
If I finished the data analysis at this moment, it would turn out that predicted limits of athletes’ abilities in some distances are greater than records noted in 2012, which is a complete nonsense. This is why it is worth examining residuals in model (3). The analysis of the figure 5 shows that for distances: 200m, 400m, 10000m and marathon residuals are negative throughout most of the Olympic Games, which proves why Ti,j < hat Ti,j for j=2, 3, 7, 8. Taking this into consideration I assumed that

As a result I obtained the following formula to calculate predicted critical times.
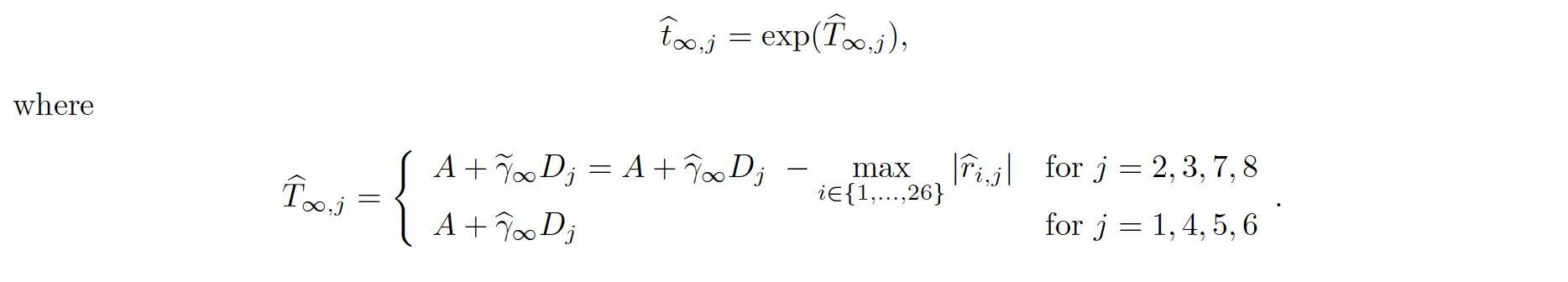
After having the correction (equation (4)) taken into consideration, I could present limits of athletes’ abilities in investigated 8 distances. The diagnostics of the antisymmetric exponential model, which fits values of the parameter γ the best (according to decreasing RSS value) proved that it didn’t fulfil each of the required assumptions. I acknowledged that, therefore, it was worth showing some kind of an interval of the limits of athletes’ abilities. This is why, I also put predictions obtained by using two other models in table 2, which held second and third place (according to decreasing RSS value).