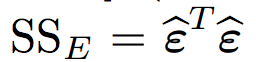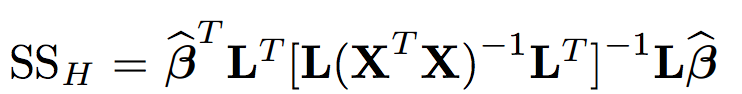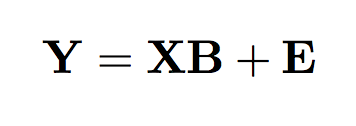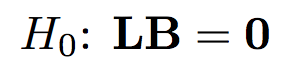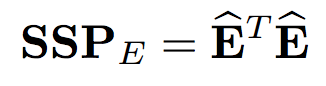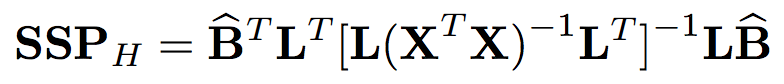Data science Archives - Page 9 of 10

Mice, post hoc tests and diffograms

May 22, 2015/in Data science /by Przemyslaw Biecek

I’ve recently worked on an interesting problem. There are two types of mice. We select three animals of each type. We want to examine an effect of given treatment on nerve cells, more specific: on their dendritic spines (small protrusions located at neurons). From each selected mouse we collect samples of its brain and we apply two different treatments to each sample. Then we take several dozen photos of each sample and we mark hundreds of dendritic spines on each photo.

We measure parameters of the spines but the measurements are not independent. We need to consider the effect of photo’s nested in the effect of brain sample nested in the effect of mouse which is in turn nested in the effect of type of mice. Our goal is to compare four experimental conditions (combination of the type of mice and the type of treatment).

How we can model this?

As we are not particularly interested in the effects of mouse, brain sample and photo, we used the random effects to describe them. The effects of mouse and treatment type are directly interesting so we used the fixed effects to describe them. All together we get mixed models, that is, the lmer function from the lme4 package.

mmodel = lmer(spine ~ type*treatment +
(1|animal:type) + (1|animal:type:sample) + (1|animal:type:sample:photo),
data=spines)

I was looking for a function for post hoc testing and I found the lsmeans function in the package bearing the same name (functionality borrowed from the LSMEANS SASa procedure).
The package allows for testing many various contrasts. For example, the following command compares all pairs using Tukey’s post hoc procedure.

ms6 = lsmeans(mmodel,  pairwise~ type*treatment, adjust="tukey")

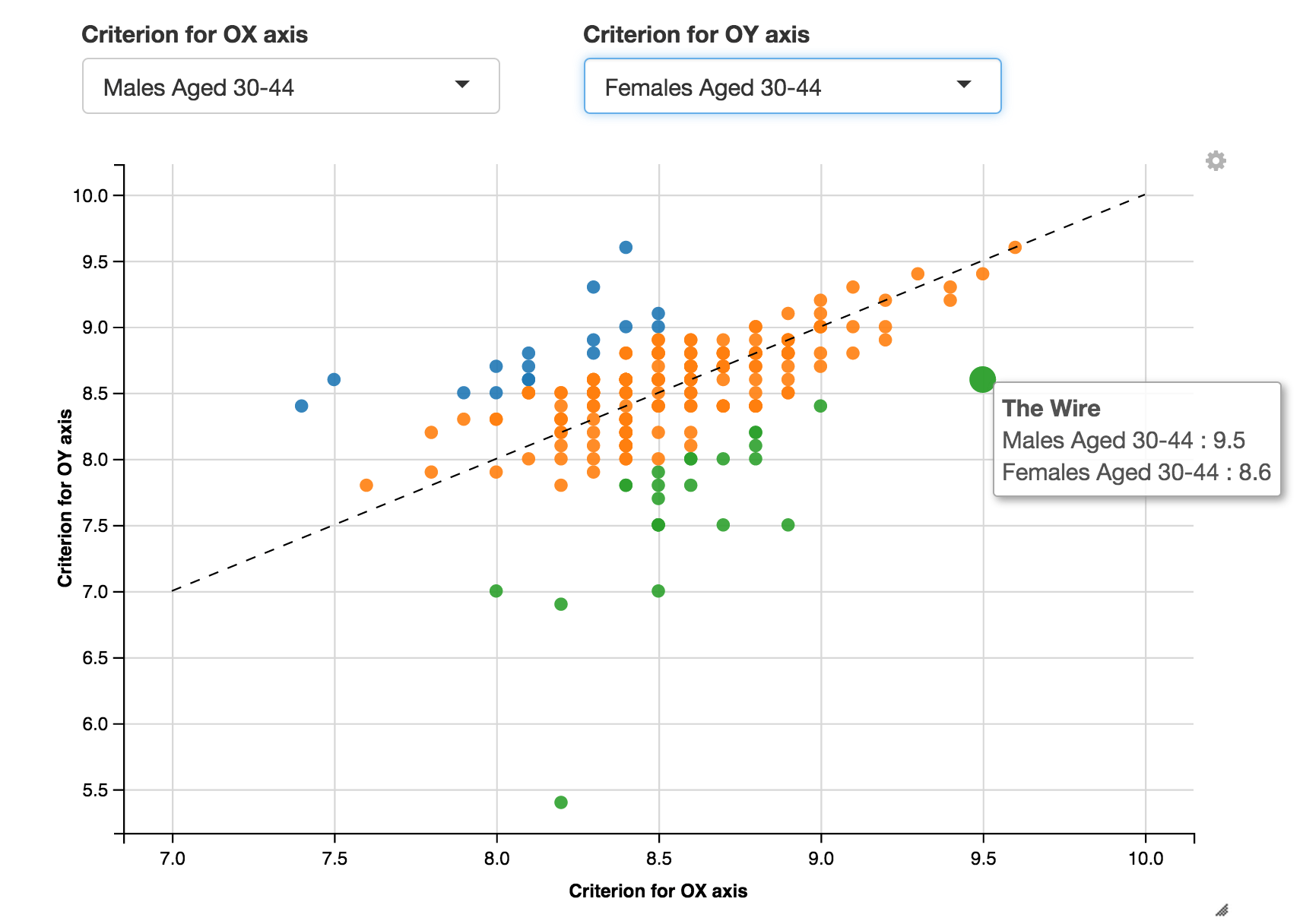
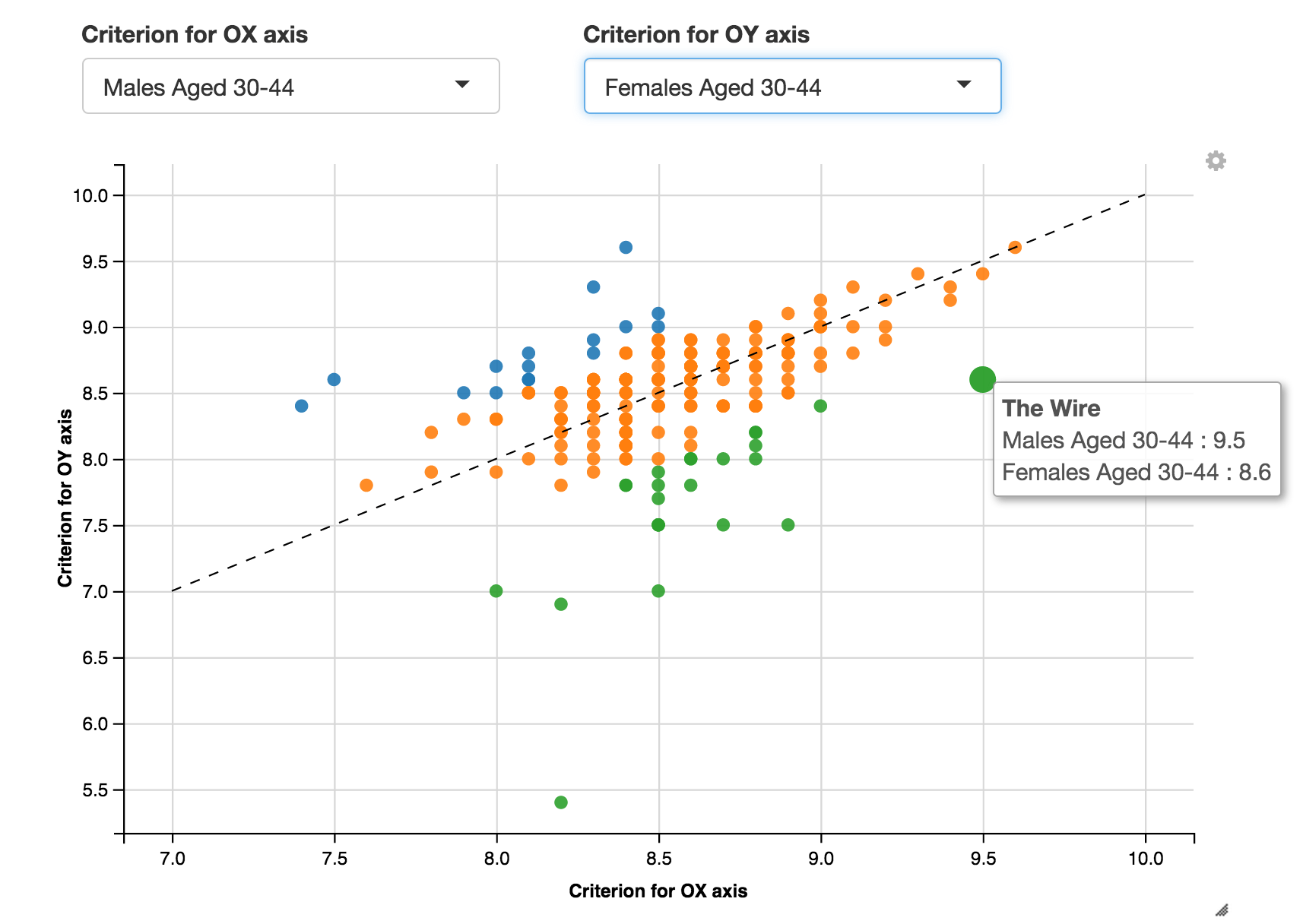
The only disadvantage of that package is lack of function for graphical presentation of the post hoc test’s results. On the other hand in SAS one can use diffograms to graphically present post hoc tests. I felt uneasy that I could not find them in R so I wrote a diffogram function myself (see the package DendriticSpineR).
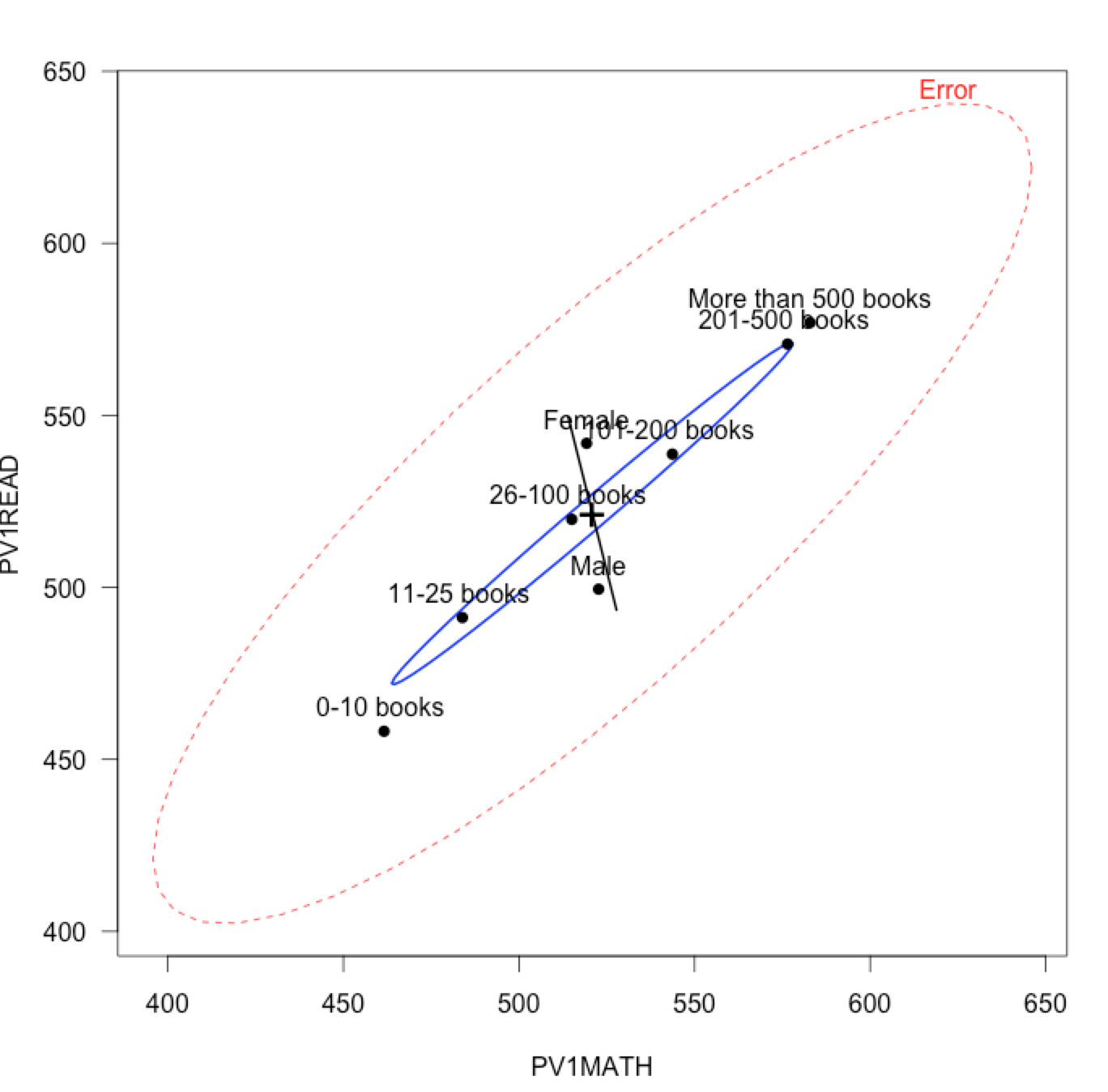
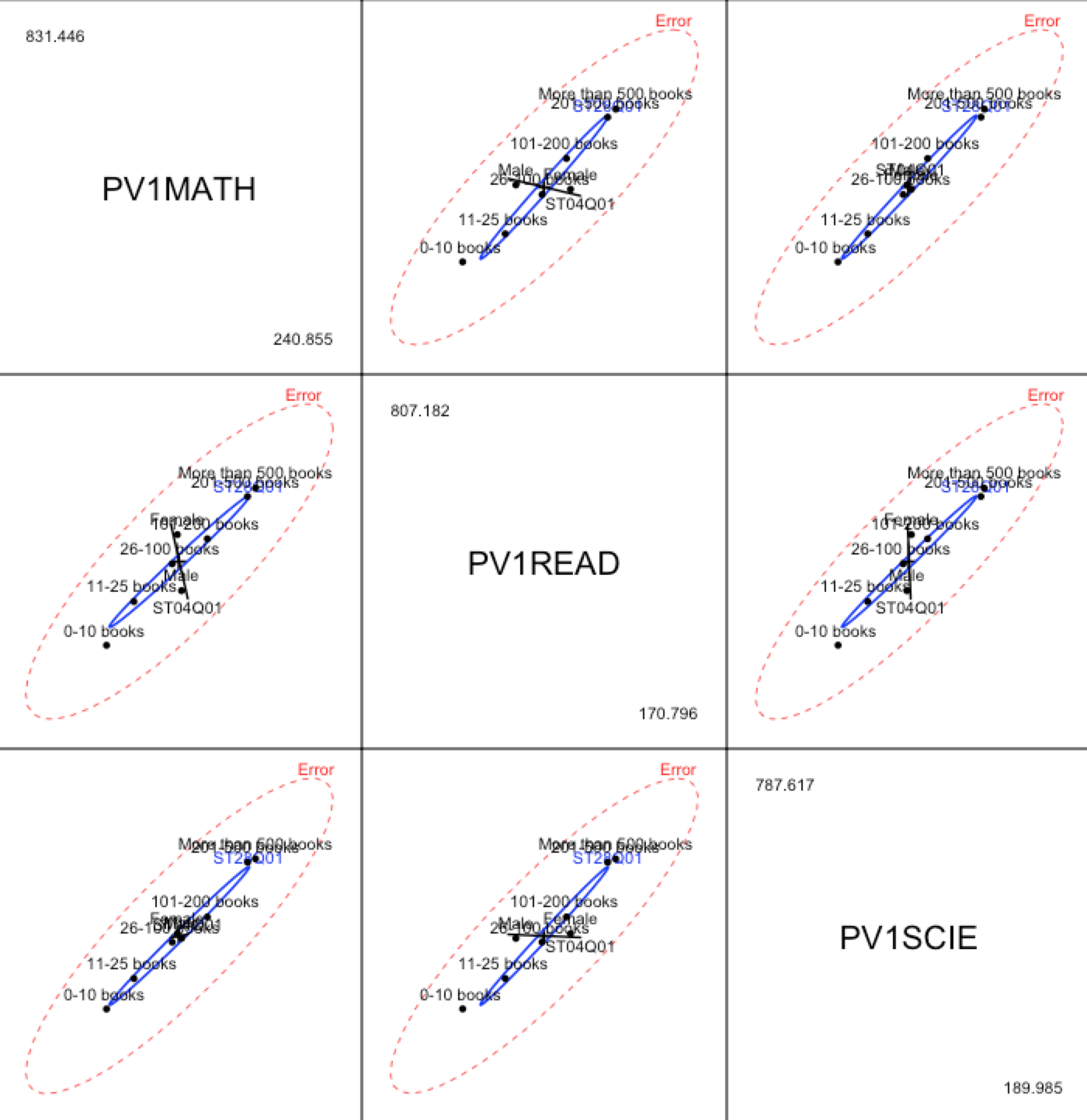
Below you can see an example diffogram.

diffogram(ms6)

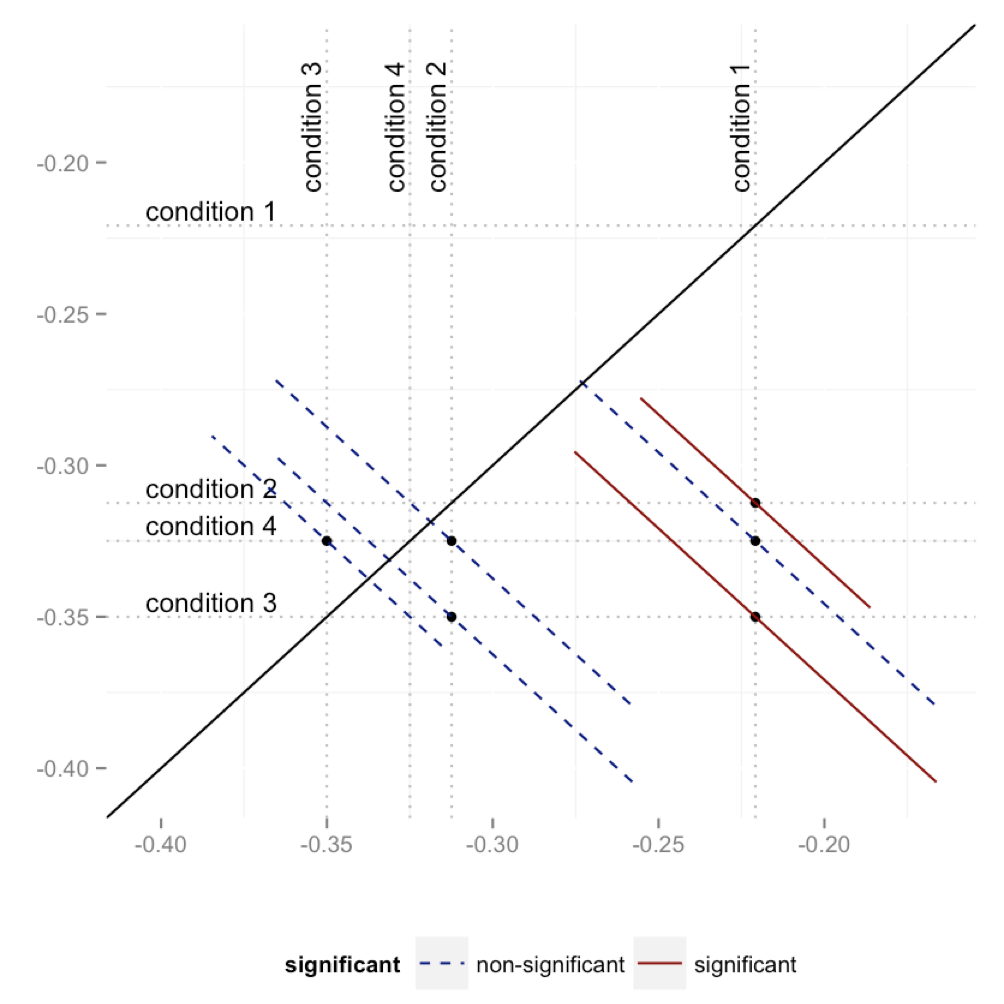
Reading diffograms is a very interesting activity. They display values of individual effects (four dashed lines on both OX and OY axes) as well as results of pair-wise tests (four means gives six pairs) and confidence intervals for the differences.
You can find more information on how to read diffograms and why they are a convenient technique for presenting post hoc tests’ results here.

Przemyslaw Biecek

The marathon of teams’ data analysis – wrap-up

May 14, 2015/in Data science /by Przemyslaw Biecek

The first team’s data analysis marathon took place on last Saturday. Almost 60 participants turned up to take part in it (representing various levels of proficiency in the art of data analysis and different regions of Poland –most were from Warsaw but there were also people from Krakow, Poznan and Biala Podlaska). They came to grips with three problems under the supervision of 8 coordinators. The marathon took 11 hours so only the tough guys persevered until the end, although there were quite many of them (over a half).

We managed to find interesting solutions to each problem (presentation of the results took two hours even though they were being shortened). The results which made the biggest impression on me were the results of the teams working on cancer data from The Cancer Genome Atlas project. It is a very difficult problem and it had to be profoundly analyzed by both molecular biologists and data scientists. The available data was quite big (RNAseq data) and it requires a lot of preliminary processing (although a lot of work was done by the package RTCGA anyway). Data cleaning itself was amazingly time-consuming and loading data almost killed the WiFi. In the middle of the marathon it seemed that we barely managed to prepare the data for the analysis and the purpose of that analysis was still a little vague.

Yet it sometimes happens so that the difficulties only make us stronger (if we struggles to overcome them). Finally cancer teams discovered some incredible relationships showing something really… surprising. We did not manage to fully explain these results (yet) and my personal guess is that they are connected with various molecular subtypes of breast cancer. The participants were so absorbed with the topic that they are still analyzing the data even the marathon has ended.
As befits people powered by data, after our meeting we carried out a survey. Those who responded to the survey were mostly very satisfied (they stressed great atmosphere, opportunity to meet interesting people and learning new tricks/methods of data analysis). They also declared their willingness to take part in another (some suggested monthly) marathons. Some organizational issues would have to be amended (more coffee, bigger rooms better adapted to the needs of teamwork) but we are already convinced that we want to organize another marathon after the summer holidays.

The survey showed that the most crucial reason for coming to the marathon was: (1) willingness to face an interesting and important challenge, (2) willingness to improve one’s skills in working with R, (3) willingness to work in a team, meet new people and make new contacts.
We would like to thank our coordinators (in the alphabetical order): Artur Kalinowski, Katarzyna Potega (CNK), Tymoteusz Wolodzko, Tomek Zozlak (IBE), Marcin Herok, Maciej Olszewski, Bartosz Wawrzynow (IIMCB), people involved in organisational preparations: Paulina Auguscik, Marcin Kosinski, Katarzyna Fak, Barbara Sozanska (MiNI), as well as our sponsor (deepsense.ai) and finally all the participants – this event would not take place if it wasn’t for you.

Przemyslaw Biecek

The marathon of teams’ data analysis

May 6, 2015/in Data science /by Przemyslaw Biecek

In just four days’ time we are going to start a marathon of teams’ data analysis. This time it’s a local Warsaw event, but next time? It’s up to us! Let us sum up what we know about that event.

CodiLime (deepsense.ai) is a sponsor.

Organizers include Smarter Poland and the Faculty of Mathematics and Information Science of the Warsaw University of Technology.
The projects are prepared in substantive cooperation with the International Institute of Molecular and Cell Biology, Educational Research Institute and Copernicus Science Centre.
The event is organized for students and graduates interested in data analysis. It is dedicated to people who want to work in a team and realize an important and interesting project; those who want to learn what are the tools and methods used by other analysts.

The problems which we are going to face are as follows:

analysis of data from the project The Cancer Genome Atlas Project (hundreds of gigabits of data – most probably we will make use of only the tip of that iceberg) with a view of determining why in some cases chemotherapy does not affect the cancer,
analysis of data from over 600 thousand Matura exams from maths with a view of factors that influence results from that exam,
segmentation and determination of a profile of an average visitor of the Copernicus Science Centre.

A link to the registration form: https://www.facebook.com/events/921016974586900/.
During the registration procedure you will be able to choose preferable issue (cancer, Matura exam, profiling) and your tools of choice. On the basis of this data we will assign participants to particular problems.
The marathon will take place at the third floor of the building of the Faculty of Mathematics and Information Science of the Warsaw University of Technology (75 Koszykowa Street). Each issue will be analyzed in a different room.

A working agenda of the meeting is as follows:

8:30 – 9:00 – registration of the participants
9:00 – 9:15 – inauguration and organizational announcements
9:15 – 9:30 – division into groups
9:30 – 12:30 – group data analysis; meanwhile the tutors walk around and help the participants
13:00 – 14:00 – a warm meal
14:00 – 18:00 – further data analysis
18:00 – 18:50 – tutors select the best solutions to be presented
18:50 – 19:00 – a short presentation of the sponsor
19:00 – 20:00 – presentation of the best solutions
Przemyslaw Biecek

Colors of cars

April 23, 2015/in Data science /by Przemyslaw Biecek

Last week we tried to find out what is the color of the cars with the highest engine power. It turned out that black and black metallic are most popular colors of the fastest cars. Yet engine power is not all. We still may explore the relation between color and brand.

Our data set auta2012 includes as many as 37 colors and 106 makes. How can we present relation between so many of them in a readable manner?
We will employ correspondence analysis which is available in R in the ca function in the ca package.
Profiles of rows and columns of the contingency matrix are presented in one space (2D in this case) in such a way that closeness of color and brand marks popularity of a given color in the offers for sale of each particular brand.

library(PogromcyDanych)
library(ca)
# converts variable names into english
setLang()
contingency = table(auta2012$Color, auta2012$Brand)
# only colors and brands with 500 or more offers
tab = contingency[rowSums(contingency) > 500, colSums(contingency) > 500]
plot(ca(tab), arrows = c(TRUE, FALSE))

The most interesting direction is set out by black and black metallic. As you can see these colors are more frequently used for Lexus and Porsche cars than for other more colorful brands.
You may find more information on correspondence analysis at http://www.jstatsoft.org/v20/i03/paper.
Przemyslaw Biecek

What color car is the fastest?

April 16, 2015/in Data science /by Przemyslaw Biecek

RECOMB 2015, a conference devoted to computational molecular biology (with emphasis on computational), came to an end yesterday. Many interesting papers were presented, yet this post was inspired by a conversation that I had the pleasure to have during dinner break.

800px-2012_NAIAS_Red_Porsche_991_convertible_(world_premiere)

We were discussing statistical relationships; one thought led to another until we reached a hypothesis that the fastest cars are red (obviously we did not mean that color has any influence on speed but rather we entertained the idea that the relation results from color and engine power-related preferences of car owners). I had my doubts but my interlocutor was rather strongly convinced of the truth of the hypothesis. As would be expected of men believing in data, we decided to explore this issue.
A package called PogromcyDanych includes a data set auta2012 with information about around 200 thousand offers for sale of cars published in 2012. Most offers specified the color and power engine of the car.
All right, let us then check what color cars have the highest engine power.
We will calculate power median breaking cars into color groups.

library(PogromcyDanych)
# this function converts polish variable names to english ones
setLang()
auta2012 %.%
group_by(Color) %.%
summarise(mKM = median(HP, na.rm=T)) %.%
arrange(-mKM) %.%
slice(1)

Hmm, white?
I did not associate this color with high speed.
Maybe we make a mistake when we calculate medians for each color separately? Maybe it would be better to check how powerful are the most powerful white cars instead of calculating the average engine power for the whole group?
Let’s see what will be the result if we choose the 90th percentile instead of median.

auta2012 %.%
group_by(Color) %.%
summarise(mKM = quantile(HP, .9, na.rm=TRUE)) %.%
arrange(-mKM) %.%
slice(1)

White metallic?
It seems that the greatest number of cars with a very high engine power can be found in the group of white cars.
But the other thing is that many of the fast white cars are also relatively old. Maybe we should analyze old and new cars separately?
We will calculate then what is the fastest color for each production year and then we will be able to check which color dominates most often.

auta2012 %.%
filter(Color!="") %.%
group_by(Color, Year) %.%
summarise(median_KM = quantile(HP, 0.9, na.rm=T),
count = n()) %.%
filter(count>20) %.%
group_by(Year) %.%
arrange(-median_KM) %.%
slice(1) %.%
group_by() %.%
arrange(-Year) %.%
as.data.frame()
## Color Year median_KM count
## 1 black 2012 396.0 22
## 2 white-metallic 2011 317.2 411
## 3 grey 2010 435.0 58
## 4 white-metallic 2009 290.8 139
## 5 grey 2008 321.8 59
## 6 grey 2007 314.5 50
## 7 white-metallic 2006 279.0 73
## 8 white-metallic 2005 311.4 68
## 9 black 2004 232.7 343
## 10 black 2003 220.0 299
## 11 brown-metallic 2002 199.0 51
## 12 brown-metallic 2001 240.4 43
## 13 black-metallic 2000 194.7 1058
## 14 brown-metallic 1999 214.4 39
## 15 brown-metallic 1998 203.0 29
## 16 graphite-metallic 1997 194.4 156
## 17 black-metallic 1996 187.5 251
## 18 black-metallic 1995 218.0 188
## 19 navy-metallic 1994 220.0 27
## 20 silver-metallic 1993 231.0 88
## 21 black-metallic 1992 217.3 102
## 22 black-metallic 1991 218.2 64
## 23 black-metallic 1990 310.0 44
## 24 black-metallic 1989 203.4 21
## 25 black 1988 246.0 23
## 26 white 1987 136.0 21

The list presented above is dominated by three colors; black, white and grey. Red is completely absent.
But let us check also what color is the most popular among cars with engine power exceeding 500 hp.

auta2012[auta2012$HP > 500,"Color"] %.%
table() %.%
sort() %.%
tail(1)

Black metallic.
Looking at the data we have to admit that the cars with most powerful engines are not red at all but rather black, grey or white.
Przemyslaw Biecek

IMDB + ggvis, a happy couple

March 26, 2015/in Data science /by Przemyslaw Biecek

Two weeks ago we showed how to scrap data from IMDB database with the use of rvest package. Last week we showed a shiny application, that compares ratings from two selected groups of users. Today we are going to finish the IMDB trilogy. This time I am going to show how to create an ggvis plot based on IMDB data.

The ggvis package has still smaller expressiveness than it’s older brother ggplot2. But, when it comes to web pages or shiny applications, the plots created in ggvis look pretty good.
Data and source codes for the shiny app and scripts presented below are available on the github webpage.
Let’s start with the data loading. In the data set ‘votesGroup’ we have average ratings for each one out of 14 groups of users. See list of these group names below.

# load the data set with average ratings in groups
load("votesGroup.rda")
# groups in the data
# [1] "Males"              "Females"            "Aged under 18"      "Males under 18"     "Females under 18"
# [6] "Aged 18-29"         "Males Aged 18-29"   "Females Aged 18-29" "Aged 30-44"         "Males Aged 30-44"
# [11] "Females Aged 30-44" "Aged 45+"           "Males Aged 45+"     "Females Aged 45+"   "serialName"

Let us compare ratings between Males and Females. These ratings are available in column names ‘Males’ and ‘Females’. We just need to convert them into numeric variables since originally they are stored as characters. Then we create a new factor variable (gr), which describes if ratings of male are higher than ratings of female, lower or similar.

# select only specific cols
group1 = "Males"
group2 = "Females"
# convert characters to numbers
xx = as.numeric(votesGroup[,group1])
yy = as.numeric(votesGroup[,group2])
gr = cut(xx - yy, c(-10,-0.5,0.5,10))
df = data.frame(x = xx, y = yy, gr = gr,
               name = votesGroup[,"serialName"])

Having this new data we are ready to plot it.
First, load the ggvis library, then create a stub of the plot with the ggvis function, and then add points with the laver_points() function. Last two lines change labels on OX and OY axes.

library(ggvis)
# here goes the plot
df %.% ggvis(x =~ x, y =~ y) %.%
  layer_points(fill = ~gr, size.hover := 200,
               fillOpacity := 0.9,
               fillOpacity.hover := 0.95) %.%
  add_axis("x", title = group1) %.%
  add_axis("y", title = group2)

Not bad.
Just three more things are missing.
We would like to add interactive labels, that are presented on hover. Below it’s done with the function labs().
Then we would like to add a diagonal to make it easier to see serials that are equally rated by both groups. To do this we create a new dataset with coordinates of this diagonal, the new dataset is plotted as a new layer by the function layer_abline().
And last we remove legend, since it does not look good.
After these changes, the final code looks like this.

# interactive labels
labs = function(data){
  if(is.null(data)) return(NULL)
  paste0("",data$name, "
 ", data$x, "
", data$y,"")
}
# diagonal line
abline_data = function (domain, intercept, slope) {
  data.frame(x = domain, y = domain * slope + intercept)
}
layer_abline = function (.vis, domain, intercept = 0, slope = 1, dash = 6, ...) {
  df = abline_data(domain, intercept, slope)
  names(df) = with(.vis$cur_props, c(x.update$value, y.update$value))
  layer_paths(.vis, data = df, ..., strokeDash := dash)
}
# here goes the plot
df %.%
  ggvis(x =~ x, y =~ y) %.%
  group_by(name) %.%
  layer_points(fill = ~gr, size.hover := 200,
               fillOpacity := 0.9,
               fillOpacity.hover := 0.95) %.%
  layer_abline(c(7,10)) %.%
  add_axis("x", title = group1) %.%
  add_axis("y", title = group2) %.%
  hide_legend(scales = "fill") %.%
  add_tooltip(labs, "hover")

Przemyslaw Biecek

You should not watch these movies with your wife / girl

March 19, 2015/in Data science /by Przemyslaw Biecek

Last week’s post showed how to download data on ratings of over 200 television series. The rating was broken down by gender and age of the user.

The application presented below allows for selection of any two age/gender groups of users and comparison of their ratings of particular television series. We can check which two series were ranked the highest and the lowest by these groups and which two series were most differently rated.
There are some interesting differences between genders and especially age groups.
Click to open and have fun!
Next week I will show you how to develop such application.

If you cannot start the application above, you can try to open it at https://smarterpoland.shinyapps.io/serialeIMDB_groups/.
Przemyslaw Biecek

R, rvest and web-harvesting

March 12, 2015/in Data science /by Przemyslaw Biecek

Data harvested from the web pages is a source of interesting information. Pulling data used to require quite a lot of resilience and misshapen Perl scripts struggling with messy sources of web pages. Today’s web pages more and more frequently comply meet the standards. There are also more and more civilized tools for parsing websites.

Source flickr

A package rvest has lately gained my sympathy. Harvesting data from web pages with that package is very easy. I would like to present it on the example of scrapping ratings from television series separately for age group and gender of the reviewer. We will make use of this data next week. Today I will only show you how to download it.
When you visit the Internet Movie DataBase (IMDB) and find the tab “user ratings” (see here for example), you will find ratings of given movies broken down by age and gender groups. When you use the package rvest to download the data and parse the html page into html tree, the whole procedure comes down to two lines.

library(rvest)
page = html("http://www.imdb.com/title/tt0903747/ratings")

We can choose only the interesting elements/nodes from that tree. In order to select particular elements we will use an extraordinary tool SelectGadget (http://selectorgadget.com/). The only thing that we need to do now is to click on the content that we want to read and the content that we want to ignore. SelectorGadget will suggest the so-called Css.selector and will highlight in yellow the elements compatible with it. The selector that we need in case of our films is “table:nth-child(11) td:nth-child(3)”.

Screenshot of the webpage with elements highlighted by SelectorGadget. All nodes that match the css selector are marked yellow.

In order to harvest the interesting data we need to:
1. Select the nodes of the html tree compatible with the selector (using the function html_nodes),
2. Extract the text from the nodes (using the function html_text). If there is something else apart from numbers, we can clean the nodes with a regular expression.
The three lines presented below will reveal to us assessments of a given movie (in this case BreakingBad) of various age groups and different genders.

nodes = html_nodes(page, "table:nth-child(11) td:nth-child(3)")
html_text(nodes)
as.numeric(gsub(html_text(nodes), pattern="[^0-9.]", replacement=""))

Seems so trivial!
Let us repeat this for all the tv series. We will check which of them are preferred by women and which by men. We can also see which series gain recognition among the younger audience and which among the older audience.
Instead of titles of the series the addresses of the web pages of IMDB service use identification numbers. The identification number for BreakingBad is tt0903747.
Where can we find the identification numbers of the movies? We can use the data set serialeIMDB from the package PogromcyDanych. It contains identification numbers of over 200 most popular television series gathered in the column imdbId.
The following code will download the webpage with ratings of each series. Then, it will extract the ratings broken down by age and gender and save it in the table called ratings.

library(rvest)
library(PogromcyDanych)
serialsToParse = levels(serialeIMDB$imdbId)
# prepare matrix for results
ratingsGroup = matrix("", length(serialsToParse), 14)
rownames(ratingsGroup) = serialsToParse
colnames(ratingsGroup) = c("Males", "Females", "Aged under 18", "Males under 18",
      "Females under 18", "Aged 18-29", "Males Aged 18-29", "Females Aged 18-29",
      "Aged 30-44", "Males Aged 30-44", "Females Aged 30-44", "Aged 45+",
      "Males Aged 45+", "Females Aged 45+")
# for all series
for (serial in serialsToParse) {
  page = html(paste0("http://www.imdb.com/title/",serial,"/ratings"))
  nodes3 = html_nodes(page, "table:nth-child(11) td:nth-child(3)")
  ratingsGroup[serial,] = gsub(html_text(nodes3)[-1], pattern="[^0-9.]", replacement="")[1:14]
}

Below you will find 10 first rows and four selected columns from the collected dataset.

ratingsGroup[1:10, c(1,2,6,12)]
Males   Females   Aged 18-29  Aged 45+
tt0903747 "9.6"  "9.3"     "9.6"        "9.3"
tt2395695 "9.4"  "9.5"     "9.5"        "9.1"
tt0795176 "9.5"  "9.5"     "9.5"        "9.4"
tt0944947 "9.5"  "9.4"     "9.6"        "9.2"
tt2356777 "9.3"  "9.1"     "9.4"        "9.0"
tt0306414 "9.5"  "8.6"     "9.4"        "9.1"
tt1475582 "9.2"  "9.4"     "9.4"        "9.0"
tt0081846 "9.4"  "9.2"     "9.2"        "9.4"
tt0141842 "9.3"  "9.0"     "9.4"        "9.1"
tt1831164 "9.1"  "9.3"     "9.4"        "7.1"

Next week I will show you an application presenting differences in assessments of female and male audience.
Przemyslaw Biecek

Canonical discriminant analyses and HE plots

February 26, 2015/in Data science /by Przemyslaw Biecek

Last week we wrote about multidimensional linear models. We discussed a case in which a k-dimensional vector of the dependent variables is related to a grouping variable. We look at matrices E and H in order to find out whether there is any relationship (see the previous blog).

We still haven’t solved one problem, though. The dependent variable has k dimensions so the matrices of H and E effects have kxk dimensions. As a result these matrices can be viewed on a plot only when they are projected onto some two-dimensional space.
But which two-dimensional subspace should we choose? We can try various projections of E and H matrices but is any of them better than the others?
Let us remember that our goal is to see whether the subgroups of the independent variable really diversify the multidimensional dependent variables. So, we will reduce dimension in the dependent variables so as to preserve the greatest between groups variation (groups determined by the independent variable).
Canonical discriminant analysis is a very popular technique used to perform such reduction of dimension. It identifies orthogonal vectors in the dependent variable space which explain the greatest possible between-group variation. If we choose the first two coordinates, we will get a subspace in which the analyzed groups are characterized by the highest between group variation.
Now we can compare matrices H and E in this particular subspace.
R program obviously has (many) packages allowing for simple construction of CDA. The one I used is called candisc.
We need to load the data, select only the data concerning Poland and build a multidimensional linear model (like the one we built a week ago).

library(PISA2012lite)
pol = student2012[student2012$CNT == "Poland",]
model = lm(cbind(PV1MATH, PV1READ, PV1SCIE)~ST28Q01+ST04Q01, pol)

Next, using the candisc function we perform CDA analysis for the chosen grouping variable (you can choose only one variable) and we build a HE plot for this variable.

library(candisc)
model2 = candisc(model, "ST28Q01")
heplot(model2)

Matrices H and E were transformed on the plot –they were multiplied by E^{-1} on the right side. As a result we can see HE^{-1} and a unit matrix. Where does this transformation come from? It is much easier to compare the blue effect ellipsis to a circle than to another ellipsis. The diagram presented above suggests that the three dimensions of the dependent variable are strongly correlated along the axis differentiating the groups of ST8Q01 variable (code for number of books at home).
Notice that if the variable has got two levels (such as gender) we need only one dimension to achieve maximum linear separation. This is why the canonical components of such variables are one-dimensional and the corresponding HE plots look in the following way.

model3 = candisc(model, "ST04Q01")
heplot(model3)

The figure on the right hand-side shows that the first canonical component is mostly influenced by reading comprehension component and also that this component is most strongly diversified by gender.
More information:
Visualizing Generalized Canonical Discriminant and Canonical Correlation Analysis
Michael Friendly and John Fox
Canonical Variate Analysis and Related Methods with Longitudinal Data
Michael Beaghen
Przemyslaw Biecek

HE plots

February 19, 2015/in Data science /by Przemyslaw Biecek

GPS helps the drivers to avoid traffic jams, yet in more advanced uses it allows for fleet management or remote drone strikes. It is just the same with visualization. Bars and dots can be used to present a set of several means but there are also more advanced uses such as presentation of differences in the covariance structures. And it’s today’s topic. But first things first.

I have recently faced the following problem (field of science: anthropology). We have skulls, both female and male, found in different places. Each skull is described by five numbers specifying distances between particular elements of the skull. What question do we want to answer? We want to test whether and to what extent the parameters are different for female and male skulls and for the skulls found in various locations.
If parameters of the skulls were expressed by one number instead of five we could solve the puzzle using a classic two-way analysis of variance.Having five parameters describing the skulls, we can approach each of them individually and solve the problem by performing five separate analysis of variances.
However, our parameters are interdependent and in this case we will get much better results if we employ models allowing for simultaneous modeling of multidimensional variables.
We face the problem of simultaneous modeling of multidimensional measurements quite often, especially when the variables we try to present are interdependent. This is the case for example during simultaneous modeling of skills (e.g. in education, measured in few subdomains like math, reading, science), financial products (prepossession vs. risk) or in industry like modeling of the amount of milk, protein and fat in the milk yield.
Is there scope for interesting plots? Let us see.
We will start from taking a quick look at the one-dimensional problem.
The standard linear model with one-dimensional response is usually as follows:

The null hypothesis in a general form can be written in the following way (L is a contrast matrix):

The test for such hypothesis is based on the quotient of two estimates. One of them is a estimate of the size of random noise

and the other one is the estimate of the size of effect

After scaling such quotient has distribution F. If the effect is considerably bigger than the distortion we consider this effect really significant. That’s it.
But how about multidimensional models?
Firstly, effect Y is multidimensional and as a result the effects are described by the coefficient matrix and the vector of random noise is also multidimensional.

The hypothesis is constructed in a very similar way. The only difference is that zero on the right side of the equation is a matrix.

Now we have reached the test phase. We proceed in the same way as in case of one-dimensional model. Firstly, we calculate the size of the effect (also sometimes called effect Hypothesis, whence H standing for hypothesis) and the scope of random noise (E for error). Now these values are symmetric matrices.

Once we have such a pair of matrices we have to face the following question: when is the matrix for effect considerably bigger than the matrix for random noise?
There are several approaches to this question but they usually come down to the analysis of the distance between the effect matrix times inverse of the error matrix and the unit matrix (in case of the null hypothesis the distance should be insignificant).

One can do this using characteristic values etc.
However, one can also visually compare these two matrices, e.g. on a plot! This is what HE plots are for.
In R program you will find tools for creation of HE plots in the heplots package. Let us see how to use them on an example.
Data on the skulls are not publicly available, so let us take as an example data from PISA study on levels of skills in three fields: mathematics, science and reading. We will check the influence of two factors, gender and numbers of books at home, on this three-dimensional vector.
Let’s go to R! We load the package and select only the data concerning Poland. Then we build a three-dimensional linear model and we draw a HE plots for it.

library(PISA2012lite)
pol = student2012[student2012$CNT == "Poland",]
model = lm(cbind(PV1MATH, PV1READ, PV1SCIE)~ST28Q01+ST04Q01, pol)
heplot(model, size="effect.size", las=1, term.labels=F)

Interestingly, the moment we look at this diagram we come to at least three conclusions:
(i) results in mathematics and reading comprehension are correlated in the residuals,
(ii) effect produced by books is rather strong and it is correlated both with the results in mathematics and reading,
(iii) effect produced by gender is also strong but its nature is different; females’ results in reading comprehension are on average much better while their average results in mathematics are a little worse.
All the relationships presented on one plot.
This is a diagram presenting matrices H and E for the pair of variables. We can display all the pairs using the pairs() function.

But what should we do when the variables are very numerous? Instead of generating dozens of diagrams we would like to present the most important information on one diagram which would sum up all the variables. In such case we might use canonical discriminant analyses which will be a topic of the next week’s post.
More information about HE plots is available:
Visual Hypothesis Tests in Multivariate Linear Models: The heplots Package for R
John Fox Michael Friendly Georges Monette
HE Plots for Multivariate Linear Models
Michael Friendly
HE Plots for Repeated Measures Designs
Michael Friendly

Przemyslaw Biecek

Mice, post hoc tests and diffograms

How we can model this?

The marathon of teams’ data analysis – wrap-up

The marathon of teams’ data analysis

The problems which we are going to face are as follows:

A working agenda of the meeting is as follows:

Colors of cars

What color car is the fastest?

IMDB + ggvis, a happy couple

You should not watch these movies with your wife / girl

R, rvest and web-harvesting

Canonical discriminant analyses and HE plots

HE plots

Contact us

Locations

Let us know how we can help

Services

Resources

About us

Support

Join our community